Тест 1.11 Чистый изгиб призматического бруса
Верификационные тесты ЛИРА-САПР / Тест 1.11 Чистый изгиб призматического бруса / Аналитическое решение: S. Timoshenko, Théorie de l’élasticité, Paris, Librairie Polytechnique Ch. Béranger, 1961, pages 284 – 289.
Аналитическое решение: S. Timoshenko, Théorie de l’élasticité, Paris, Librairie Polytechnique Ch. Béranger, 1961, pages 284 – 289.
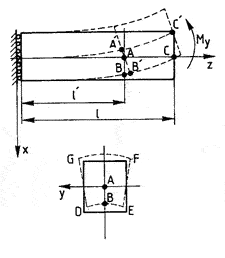
Геометрия:
 |
l = 6 м; a = b = 1 м; l’ = (2/3)l. |
Характеристика материала: Е = 2 х 105 МПа, ν = 0.3.
Граничные условия: На плоскости проходящей через точку В: w=0,
в точке В: w = u = v = 0, θZ = 0.
Нагрузки: В точке С приложен момент вокруг оси Y, My = 4/3 x 107 Нм.
РЕЗУЛЬТАТЫ РАСЧЕТА:
|
Точка |
Искомая величина |
Аналитическое решение |
Результаты расчета (ЛИРА) |
Погрешность,% |
|
А |
uA, м |
-4 x 10-4 |
-3,836 x 10-4 |
4,1 |
|
В |
wB, м |
2 x 10-4 |
1,918 x 10-4 |
4,1 |
|
F и G |
vF = - vG, м |
0,15 x 10-4 |
0,14455 x 10-4 |
3,63 |
|
D и E |
vD = - vE, м |
-0,15 x 10-4 |
-0,14455 x 10-4 |
3,63 |
Количество узлов:325.
Количество элементов:208.
Комментарии