История версий
LIRA-FEM
- Компоненты технологии ВIM
- Создание и корректировка модели
- Создание и корректировка расчетной модели
- Расчетные возможности
- Инструменты анализа свойств и результатов расчета
- Проектирование железобетонных конструкций
- Проектирование стальных конструкций
- Грунт
- Конструктор сечений универсальный
- Создание чертежей
- Документирование
- Региональные настройки
- Другие улучшения
Расчетные возможности
Усовершенствования расчетных возможностей
-
Актуализирован модуль динамики (32) в соответствии с требованиями “СНРА 20.04-2020. Строительные нормы Республики Армения. Сейсмостойкое строительство. Нормы проектирования”.
-
Для объемных итерационных КЭ добавлена информация о НДС сечения, которая позволяет анализировать состояние основного и армирующего материалов.
-
Для нелинейных упругих связей (КЭ 295, 296) реализовано вычисление окончательных жесткостей.
Расчет реакций
Настройки расчета
-
Реализовано альтернативное правило знаков деформаций для КЭ 55, 255, 265 и 295. Смысл нового правила заключается в том, что если узлы перемещаются вдоль некой оси локальной системы координат элемента навстречу друг другу (сжатие), то деформация вдоль этой оси имеет знак «-», а если узлы перемещаются друг от друга (растяжение), то деформация имеет знак «+». Если проекции узлов на эту ось совпадают, то знак деформации будет зависеть от порядка перечисления узлов при задании элемента т. е. также как и определялся ранее.
Примечание:
Ранее деформации вычислялись как разница перемещений 2-го и 1-го узла. Т.е. знак деформации зависел от порядка перечисления узлов при задании элемента.
-
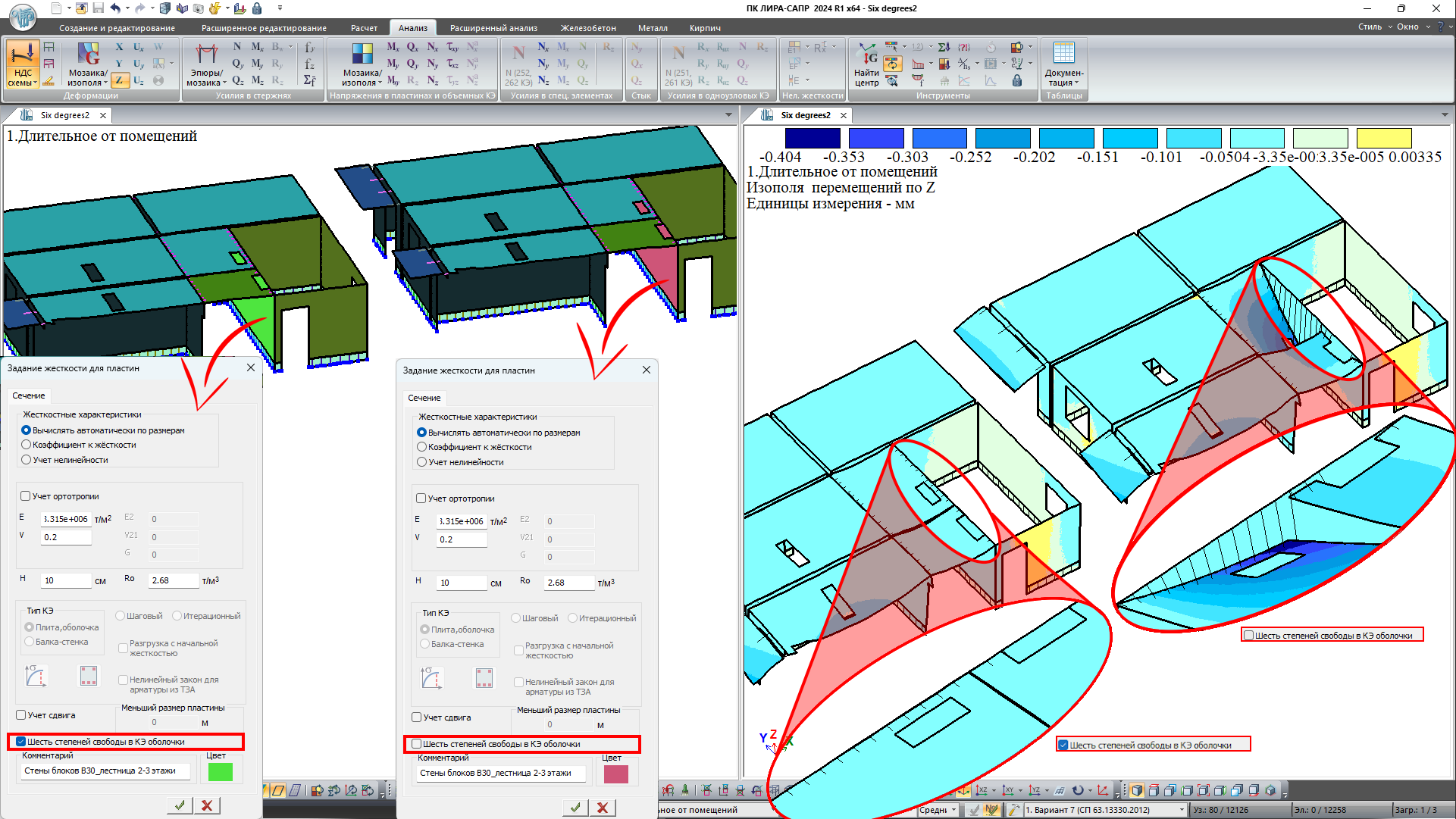
При расчете пластинчатых систем стало возможным для отдельных конечных элементов оболочки задание шестой степени свободы (поворот UZ относительно оси ортогональной плоскости пластины).
Учет ортотропии
Добавлена проверка и ограничение на заданные характеристики жесткости ортотропии. Необходимо, чтобы жесткость была положительной:
-
для пластинчатых КЭ ν12 ≥ 0, ν21 ≥ 0, ν12*ν21 < 1;
-
для объемных КЭ ν12 ≥ 0, ν21 ≥ 0, ν13 ≥ 0, ν31 ≥ 0, ν23 ≥ 0, ν32 ≥ 0,
ν12*ν21 + ν23*(ν12*ν31 + ν32) + ν13*(ν21*ν32 + ν31) < 1
Условия того что матрица физических постоянных для ортотропии положительно определенная:
-
для пластинчатых КЭ E1*E2 > (0.5*(E1*ν12+E2*ν21))^2;
-
для объемных КЭ
E1*E2*(1-ν23*ν32)*(1-ν13*ν31) > (0.5*(E1*(ν12+ν13*ν32)+E2*(ν21+ν31*ν23)))^2
E1*E3*(1-ν23*ν32)*(1-ν12*ν32) > (0.5*(E1*(ν13+ν12*ν23)+E3*(ν31+ν21*ν32)))^2
E2*E3*(1-ν13*ν31)*(1-ν12*ν32) > (0.5*(E2*(ν23+ν13*ν21)+E3*(ν32+ν12*ν31)))^2
Нелинейные пользовательские сечения
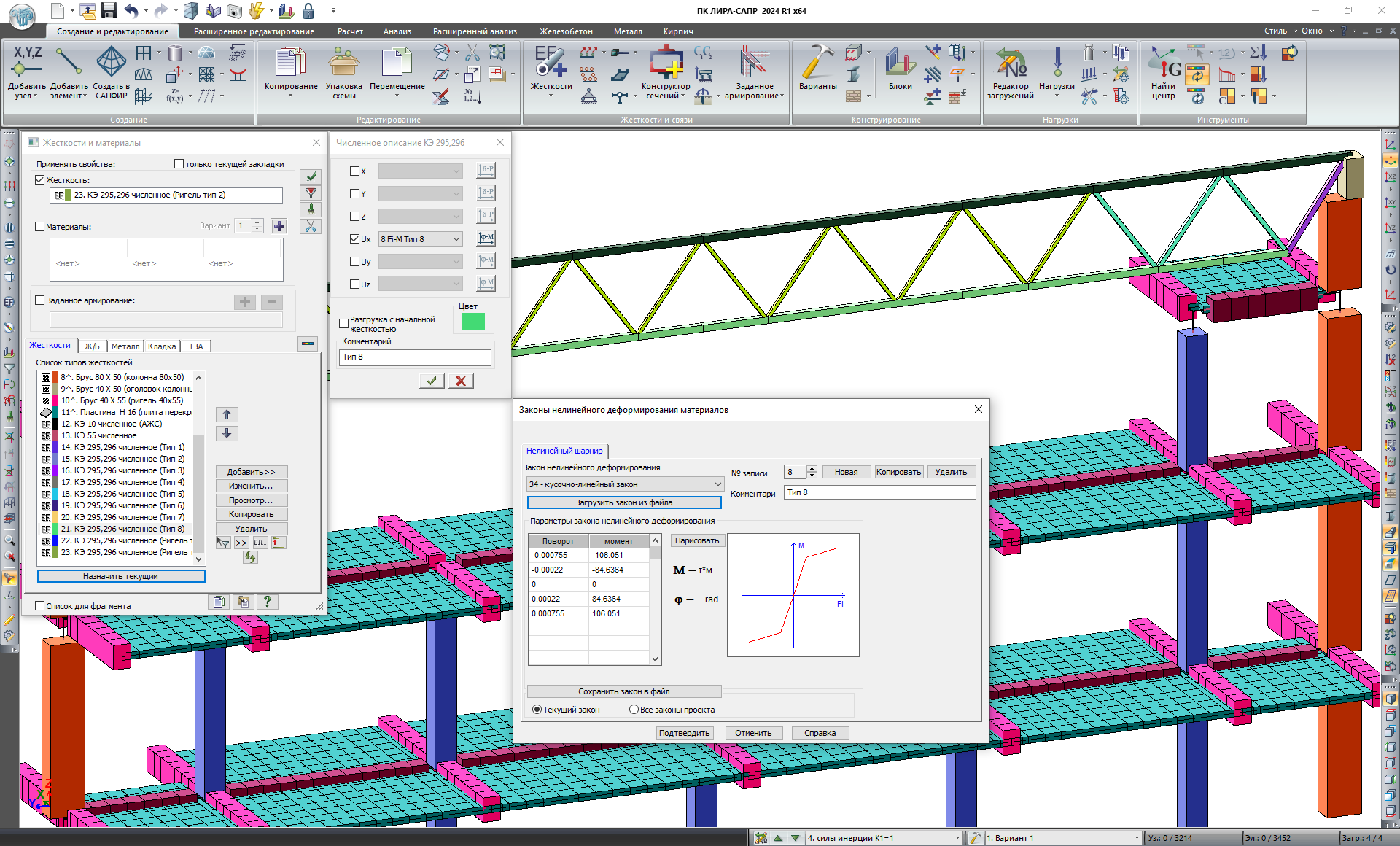
Реализована возможность расчета физически нелинейных стержневых конечных элементов для которых назначено сечение произвольного очертания и состава, созданное с помощью системы “Конструктор сечений универсальный”. Элементы с таким сечением могут быть физически нелинейными шаговыми, итерационными с разгрузкой с начальной жесткость и итерационными без учета разгрузки.
Новый вид усилия
Реализовано вычисление нового вида усилия - аналога перерезывающей силы для стесненного кручения (признак схемы 6). Изгибно-крутильный момент вычисляется в расчетных сечениях стержня, а также для него строятся эпюры по длине стержней для КЭ 7. Данный вид усилия необходим для определения касательных напряжений при проверке несущей способности элементов подверженных кручению.
Нелинейная работа грунта
-
Реализован учет максимального сопротивления грунта для нелинейной работы упругого основания стержней и пластин.
Раньше под нелинейной работой упругого основания стержней и пластин подразумевалось только то, что С1/С2 выключалась из работы при отрыве (односторонняя работа). Теперь в дополнение к односторонней работе можно задать еще и ограничение на максимальное сопротивление грунта на сжатие. Т.е. теперь есть два варианта работы упругого основания:
- односторонняя работа и отсутствие ограничения на максимальное сопротивление грунта;
- односторонняя работа и ограничение на максимальное сопротивление грунта на сжатие.
-
Добавлена возможность получать предельное значение расчетного сопротивления из расчета системы “ГРУНТ”.
Важно!
Максимальное сопротивление грунта должно быть отрицательным значением. Если данные отсутствуют или значение больше или равно нулю, то в расчет принимается условие, что максимальное сопротивление грунта не задано.
Новые типы АЖТ
Реализованы новые типы АЖТ.
Теперь АЖТ может быть одним из следующих типов:
- Все степени свободы
- X, Y, Z, UX, UY, UZ
- Z, UX, UY
- Y, UX, UZ
- X, UY, UZ
- X, Y, UZ
- X, Z, UY
- Y, Z, UX
- X, Y, UX, UY, UZ
- X, Z, UX, UY, UZ
- Y, Z, UX, UY, UZ
Направления степеней свободы соответствуют направлениям локальной системы координат ведущего узла.
Раньше АЖТ было только 1-го типа «Все степени свободы». Это означало, что кроме кинематических связей между X, Y, Z, UX, UY, UZ ведомый и ведущий узел были связаны одинаковыми значениями депланации (6-й признак схемы) и температуры (15-й признак схемы).
2-й тип АЖТ накладывает только кинематические связи между X, Y, Z, UX, UY, UZ.
Типы АЖТ 3-5 связывают перемещения ведомого и ведущего узла при их выходе из соответствующей плоскости. Соответственно в этой плоскости перемещения ведомого и ведущего узла независимы.
Типы АЖТ 6-8 связывают перемещения ведомого и ведущего узла в соответствующей плоскости. Соответственно при выходе из этой плоскости перемещения ведомого и ведущего узла независимы.
Типы АЖТ 9-11 делают перемещения ведомого и ведущего узла независимыми только вдоль соответствующей оси.
Теперь узел может быть ведущим сразу для нескольких АЖТ. Продиктовано это следующим.
Рассмотрим моделирование пересечения плиты со стеной, где плита «оставляет след» в виде АЖТ в стене, а стена «оставляет след» в виде АЖТ в плите.
Раньше схема на рисунке моделировалось тремя АЖТ:
1, 4, 5, 48, 51
2, 6, 7, 47, 50
3, 8, 9, 46, 49
Теперь это можно смоделировать с помощью шести АЖТ. Это позволит освободить степени свободы в АЖТ в направлениях не требующих сдерживания. Например, чтобы узлы плиты и стены, находящиеся в АЖТ, могли свободно перемещаться от температурного нагрева.
1, 4, 5 (тип АЖТ 3. Z, UX, UY)
1, 48, 51 (тип АЖТ 5. X, UY, UZ)
2, 6, 7 (тип АЖТ 3. Z, UX, UY)
2, 47, 50 (тип АЖТ 5. X, UY, UZ)
3, 8, 9 (тип АЖТ 3. Z, UX, UY)
3, 46, 49 (тип АЖТ 5. X, UY, UZ)
Т.е. 1, 4, 5 - это неизгибаемое тело в плоскости ХОУ, но может в этой плоскости деформироваться,
А 1, 48, 51 — это неизгибаемое тело в плоскости УOZ, но может в этой плоскости деформироваться
Внимание!
При чтении файлов задач предыдущих версии все АЖТ имеют 1-й тип (все степени свободы).
Ведомый узел может входить только в одно АЖТ и ведомый узел не может являться ведущим.
Конечный элемент "стык"
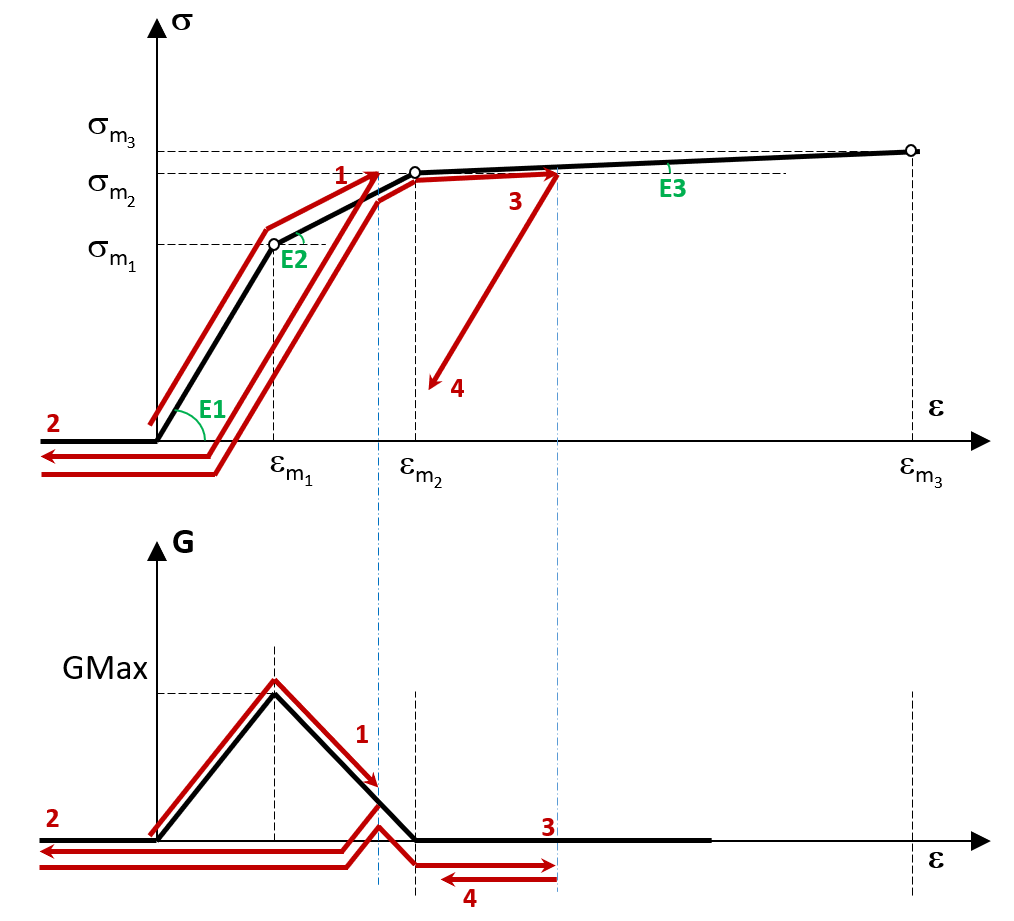
Для КЭ стыка добавлена опция "Разгрузка с начальной жесткостью". Разгрузка выполняется по упруго-пластической модели с начальной жесткостью от точки текущего состояния. Повторная загрузка происходит по ветви предыдущей разгрузки, что возвращает состояние стыка в точку с максимальной деформацией, которая была достигнута ранее. Сдвиговая жесткость КЭ стыка связана с вертикальной жесткостью зависимостью, показанной на рисунке ниже.
Pushover Analysis
-
Для расчета методом Pushover Analysis добавлена возможность задания пользовательских шагов приложения горизонтальной сейсмической нагрузки и учета коэффициента диссипации.
-
В расчете методом Pushover Analysis реализована возможность использовать итерационные КЭ, ранее использовались только шаговые. Например, данная возможность позволяет учитывать локальную пластичность с помощью введения нелинейных шарниров и неупругих связей.
Сейсмоизоляторы
Для КЭ трения 263/264 реализована опция "Разгрузка с начальной жесткостью". Опция позволяет реализовать гистерезисное поведение КЭ при циклическом нагружении: в момент изменения направления движения (когда скорость равна 0) происходит срабатывание силы трения T=N*mf (mf - заданный в параметрах жесткости коэффициент трения). КЭ трения при включении опции "разгрузка с начальной жесткостью" позволяет описать, к примеру, поведение фрикционного сейсмоизолятора, а при параллельном соединении с КЭ упругой связи - фрикционный маятниковый сейсмоизолятор.
Коэффициенты диссипации
-
Добавлено вычисление коэффициентов диссипации по формам для динамических модулей 41 и 64 (вычисляется на основании коэффициентов диссипации, заданных для элементов).
Примечание: в версии Лира-САПР 2022 R2 при расчёте на акселерограммы сейсмического воздействия с использованием 27 и 29 модулей динамики для расчетных моделей, состоящих из элементов или подсистем с различными демпфирующими свойствами, был реализован расчёт эквивалентного затухания по j-ой собственной форме колебаний по следующей формуле:
ξj={φj}T*∑[ξK]i*{φj}/{φj}T*[K]*{φj}
где {φj} – вектор j-й формы колебаний, [K] – матрица жесткости модели, ∑[ξK]i – матрица жесткости для i-го элемента или подсистемы, умноженная на коэффициент диссипации (коэффициент демпфирования в долях от критического) для этого элемента.
-
Добавлена возможность использовать раздельно коэффициенты диссипации для каждого динамического загружения в модулях динамики 27/29 и 41/64. Для этих модулей добавилась возможность ограничивать коэффициент диссипации: для 27 и 29 – максимальный коэффициент диссипации, для 41 и 64 – минимальное и максимальное Nu.
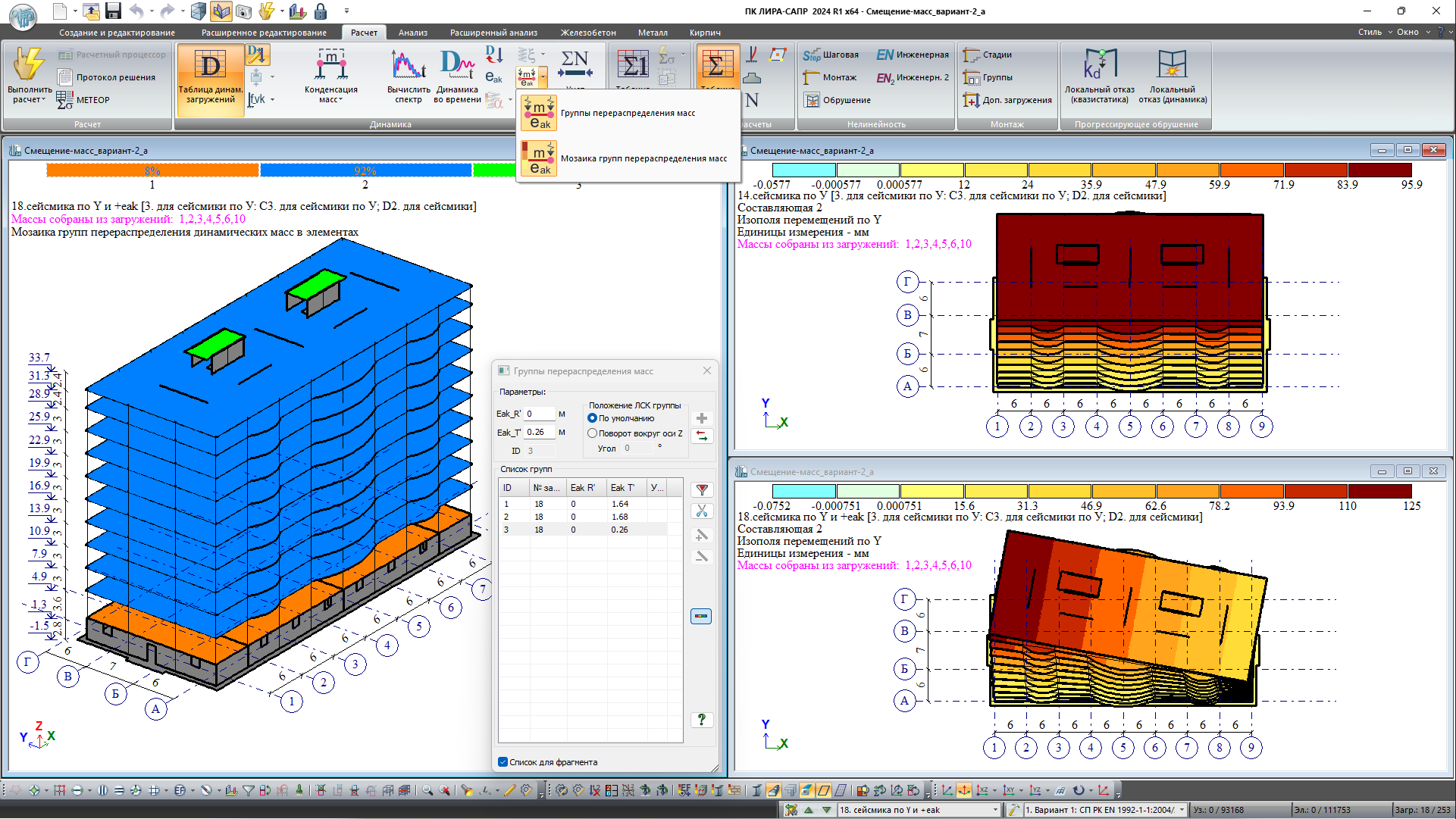
Перераспределение масс
Реализована процедура перераспределения масс. Для каждого спектрального динамического загружения и для динамики во времени можно задать набор групп перераспределения масс. Данная функциональность позволяет выполнить требования нормативных документов, касающихся учета эффектов кручения, вызванных неопределенностями в расположении масс и пространственными вариациями сейсмического воздействия.
Каждая группа имеет такие параметры:
- Положение локальной системы координат группы. Возможны два варианта задания положения этой системы координат: по умолчанию и задание угла поворота вокруг глобальной оси Z.
- Смещение масс вдоль локальной оси R` (Eak_R`).
- Смещение масс вдоль локальной оси T` (Eak_T`).
- Список элементов для формирования группы.
Положение ЛСК группы по умолчанию определяется следующим образом:
- для однокомпонентных сейсмических воздействий – направление местной оси Х определяется как проекция сейсмического воздействия на плоскость ХOY глобальной системы координат.
- для трехкомпонентных сейсмических воздействий с радиальными составляющими – направление местной оси Х совпадает с направлением радиальной составляющей сейсмического воздействия;
- для других спектральных динамических воздействий и динамики во времени – местная система координат группы совпадает с глобальной системой координат.
Цель перераспределения масс – сместить центры масс на заданные величины смещений Eak_R` и Eak_T`.
Важно!
В группе перераспределяются массы, полученные с нагрузок и весов масс, приложенных на элементы и непосредственно на внутренние узлы группы. Внутренние узлы группы - это узлы, которые принадлежат только элементам группы. Для сбора масс элемента группы в его узлы, используется диагональная матрица масс, независимо от того какой тип матрицы был задан.